浮点数运算有误差的问题

# 现象

话不多说，直接上图！

通过上图我们知道，答案是不相等，而且还有一个很神奇的问题，0.1+1-1 也不等于 0.1，并且先加后减和先减后加的结果竟然还不一样！

# 原因

其实这个问题不能完全怪 JavaScript，导致这样的问题是因为 JavaScript 中使用基于 IEEE 754 标准的浮点数运算，所以会产生舍入误差。
也就是说所有遵循 IEEE 754 标准的语言进行浮点数运算的时候，都会有这个问题。

# 产生误差过程

接下来我们来揭秘产生误差的过程。
首先这里我们需要知道，浮点数运算的时候需要先转成二进制，然后再进行运算。那么十进制浮点数是如何转二进制的呢？

浮点数转二进制的过程如下：
1.整数部分采用 /2 取余法

3 => 3/2 = 1 余 1  
1 => 1/2 = 0 余 1  
所以 3（十进制）= 11（二进制）
复制代码

1
2
3
4

4 => 4%2 = 2 余 0  
2 => 2%2 = 1 余 0  
1 => 1%2 = 0 余 1  
所以 4（十进制）= 100（二进制） 
复制代码

1
2
3
4
5

2.小数部分采用 *2 取整法

0.5 => 0.5*2 = 1 取整 1
0.5（十进制）= 0.1（二进制）
复制代码

1
2
3

0.1 => 0.1*2 = 0.2 取整 0
0.2 => 0.2*2 = 0.4 取整 0
0.4 => 0.4*2 = 0.8 取整 0
0.8 => 0.8*2 = 1.6 取整 1
0.6 => 0.6*2 = 1.2 取整 1
0.2 => 0.2*2 = 0.4 取整 0
0.4 => 0.4*2 = 0.8 取整 0
0.8 => 0.8*2 = 1.6 取整 1
0.6 => 0.6*2 = 1.2 取整 1
...发生循环
得到结果 0.1（十进制）= 00011001100110011001100110011... (0011)循环（二进制）
复制代码

1
2
3
4
5
6
7
8
9
10
11
12

同理，既有整数又有小数的数值进行二进制转换，就是分别对整数和小数部分进行二进制转换，再相加即可。

上面的例子中可以看到 0.1 转二进制会发生无限循环，而 IEEE 754 标准中的尾数位只能保存 52 位 有效数字（具体原因我们稍后讲解），所以 0.1 转二进制就会发生舍入，所以就产生了误差。

在讲解运算过程之前，我们需要 2 个前置知识：

十进制浮点数转换二进制后尾数的 52 位 有效数字是从第一个 1 开始向后保留 52 位 有效数字，所以接下来你会发现 0.1 和 0.2 保留 52 位 尾数后长度会不同。
在舍入的过程中，遵循 0 舍 1 入 的规则。
下面的过程中为了方便大家理解，我对所有的保留 52 位 尾数后后面没有 52 位 的情况进行了补零，对部分数字为了方便运算进行了超过 52 位 的补充和转换（比如 1）。

接下来我们一起看一下示例中的运算过程：

0.1
转二进制
0.0001100110011001100110011001100110011001100110011001100110011
保留52位尾数
0.00011001100110011001100110011001100110011001100110011010

0.2
转二进制
0.001100110011001100110011001100110011001100110011001100110011
保留52位尾数
0.0011001100110011001100110011001100110011001100110011010

进行相加
0.00011001100110011001100110011001100110011001100110011010
0.0011001100110011001100110011001100110011001100110011010
----------------------------------------------------------
0.01001100110011001100110011001100110011001100110011001110
相加后的结果保留52位尾数
0.010011001100110011001100110011001100110011001100110100
转十进制
0.30000000000000004
复制代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

接下来是 0.1+1-1 的运算过程：

0.1
转二进制
0.0001100110011001100110011001100110011001100110011001100110011
保留52位尾数
0.00011001100110011001100110011001100110011001100110011010

1
转二进制并保留52位尾数
1.0000000000000000000000000000000000000000000000000000

进行相加
0.00011001100110011001100110011001100110011001100110011010
1.0000000000000000000000000000000000000000000000000000
----------------------------------------------------------
1.00011001100110011001100110011001100110011001100110011010
相加后的结果保留52位尾数
1.0001100110011001100110011001100110011001100110011010
再减1
0.00011001100110011001100110011001100110011001100110100000
转十进制
0.10000000000000009
复制代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

接下来是 0.1-1+1 的运算过程：

0.1
转二进制
0.0001100110011001100110011001100110011001100110011001100110011
保留52位尾数
0.00011001100110011001100110011001100110011001100110011010

1
转二进制并保留52位尾数
1.0000000000000000000000000000000000000000000000000000

进行相减，这里其实等价于 1-0.1 转负数
为了方便相减，我们将 1 的二进制进行转换和补零
0.11111111111111111111111111111111111111111111111111111120
0.00011001100110011001100110011001100110011001100110011010
----------------------------------------------------------
0.11100110011001100110011001100110011001100110011001100110 这里是一个接近 0.9 的负数
相减后的结果保留52位尾数
0.11100110011001100110011001100110011001100110011001101

此时 -0.9+1 等价于 1-0.9
同样，为了方便相减，我们将 1 的二进制进行转换和补零
0.11111111111111111111111111111111111111111111111111112
0.11100110011001100110011001100110011001100110011001101
-------------------------------------------------------
0.00011001100110011001100110011001100110011001100110011
相减后的结果保留52位尾数
0.00011001100110011001100110011001100110011001100110011000
转十进制
0.09999999999999998
复制代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

至此，我们就搞清楚了示例中的运算过程，从而知道了出现这些情况的原因，接下来，我们聊一下 IEEE 754，从而解开:

什么是尾数位
为什么是 52 位尾数位
为什么 0 舍 1 入

以及更多的浮点数神秘面纱~

# IEEE 754

IEEE 754 中双精度浮点数使用 64 bit 来进行存储：

第一位存储符号表示正负号 0 正 1 负
2-12位存储指数表示次方数
13-64位存储尾数表示精确度

符号位没有什么可说的，就是用来表示正负数的。
指数位表示次方数，这里的次方数是以当前的进制数为底，比如次方数为 5：

如果当前为十进制，就是 10 的 5 次方
如果当前为二进制，就是 2 的 5 次方

尾数位储存尾数表示精确度，用来表示一个大于等于 1 小于 2 的数值

综上所述，如果我们以 s 表示正负号，h 表示进制数，e 表示次方数，f 表示尾数，则浮点数 value 可以表示为：

value=s∗f∗hevalue = s*f*h^evalue=s∗f∗he

相信到了这一步，小伙伴们对指数位和尾数位的理解会更清楚一点，也解释了前两个问题。

尾数位就是 64 bit 浮点数存储尾数的部分，可以表示数值的精确度
52 位 是在 IEEE 754 标准制度的时候规定如此

而我们上面直接转二进制运算的情况下，实际上是糅合了指数位和尾数位的一个结果，所以我们保留 52 位，是在第一个 1 后面保留 52 位 有效数字。
不知道你有没有发现一个问题：尾数位只有 52 位，但是我们现在在第一个 1 后面保留 52 位 有效数字，那再加上前面的 1 不就是 53 位 位了吗？
这是因为，尾数部分的整数部分一定是一个 1,那为了充分利用 52 位 空间表示更高的精确度，可以把一定等于 1 的整数部分省略，52 位 都用来表示小数。

# 最大安全整数

同理，因为只有 52 位 尾数，所以 JavaScript 中的最大安全整数是 2^53-1，其中 53 是 52 位 尾数加上前面省略的 1，而 -1 是因为 2^53 已经是一个边界值了，大于它的值会和它相等，所以最大的安全整数是 2^53-1。

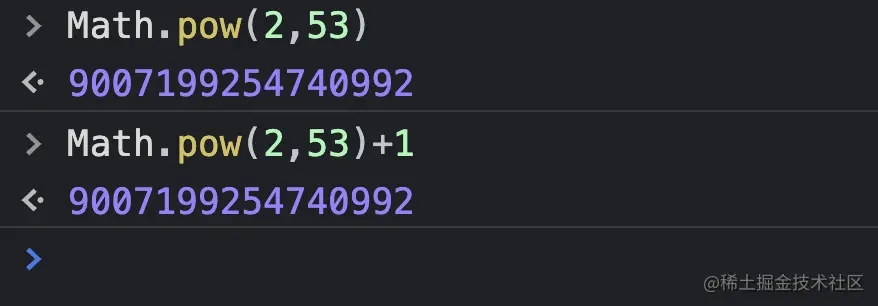
# 舍入规则

IEEE 754 标准列出4种不同的方法：

舍入到最接近：舍入到最接近，在一样接近的情况下偶数优先（Ties To Even，这是默认的舍入方式）：会将结果舍入为最接近且可以表示的值，但是当存在两个数一样接近的时候，则取其中的偶数（在二进制中是以0结尾的）。
朝+∞方向舍入：会将结果朝正无限大的方向舍入。
朝-∞方向舍入：会将结果朝负无限大的方向舍入。
朝0方向舍入：会将结果朝0的方向舍入。

第一种规则（也就是默认的舍入方式）可以简单理解为我们常用的 四舍五入，而转化到我们这里的二进制浮点数运算，就是 0 舍 1 入。

# 解决方案

使用 JavaScript 提供的最小精度值判断误差是否在该值范围内
Math.abs(0.1 + 0.2 - 0.3) <= Number.EPSILON
转为整数计算，计算后再转回小数
保留几位小数比如金额，只需要精确到分即可
使用别人的轮子,例如：math.js
转成字符串相加（效率较低）

# 参考文章链接

用了一天时间，我终于彻底搞懂了 0.1+0.2 是否等于 0.3！ (opens new window)

← 常用的位运算符有哪些 typeof和instanceof的区别→